The Normal Distribution is the commonest and the most useful continuous probability distribution. Many statistical tests require that the distribution is normal or nearly normal. Several tools are available to assess the normality of data including: using a histogram to visually explore the data, producing a normal probability plot, and carrying out an Anderson-Darling normality test. All these tools are easy to use in Minitab statistical software.
Histograms
Histograms are efficient graphical methods for describing the distribution of data. It is always a good practice to plot your data in a histogram after collecting the data. This will give you an insight about the shape of the distribution and whether it is normal or not. If the data is symmetrically distributed and most results are located in the middle, we can say that the data is normally distributed.
Suppose that a line manager is seeking to assess how consistently a production line is producing. He is interested in the weight of a food products with a target of 50 grams per item. He takes a random sample of 40 products and measures their weights.
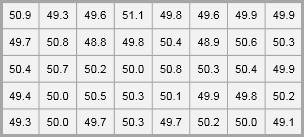
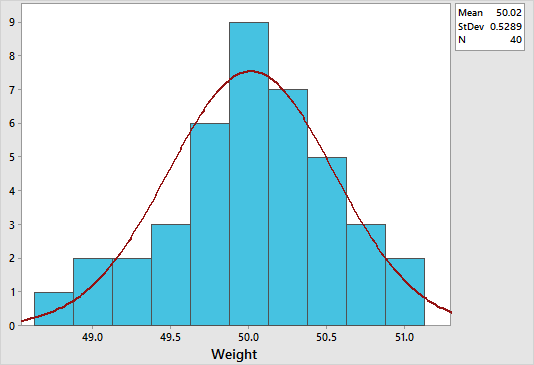
For this example, we may use the product weight worksheet. Remember to copy the data from the Excel worksheet and paste it into the Minitab worksheet. To create a histogram in Minitab, select Graph > Histogram > With Fit, specify the column of data to analyze, in this case ‘product weight’, and then click OK. The figure below shows a histogram which suggests that the data is normally distribution. Notice how the data is symmetrically distributed and concentrated in the center of the histogram.
Normal Probability Plots
We can also construct a Normal Probability Plot to test the assumption of normality. This provides a more decisive approach for deciding if a data set is normally distributed. All points for a normal distribution should approximately form a straight line that falls between 95% confidence interval limits.
To create a normal probability plot in Minitab, select Graph > Probability Plot > Single, specify the column of data to analyze, leave the distribution option to be normal, and then click OK. Here is a screenshot of the example result for our previous product weight example.
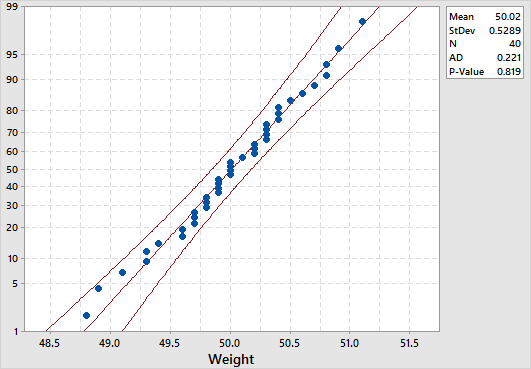
The normal distribution is a good fit if the data points approximately follow a straight line. In our example, the data points approximately follow a straight line that falls mainly between the 95% confidence interval limits, and so it can be concluded that the data is normally distributed.
Anderson-Darling Normality Test
The Anderson-Darling Normality Test measures how well the data follow the normal distribution (or any particular distribution). It is a statistical test that compares the actual distribution with the theoretical normal distribution. A lower p-value than the significance level (normally 0.05) indicates a lack of normality in the data (regardless of the AD value). Remember to keep your eyes on the histogram and the normal probability plot in conjunction with the Anderson-Darling test before making any decision.
To conduct an Anderson-Darling normality test in Minitab, select Stat > Basic Statistics > Normality Test, specify the column of data to analyze, then specify the test method to be Anderson-Darling, and then click OK.
The p-value in our product weight example is 0.819 which suggests that the data follow the normal distribution. Note that both the graphical summary and the probability plot displays Anderson-Darling normality test results by default.